Um grafo é ponderado quando suas arestas possuem um peso. O que significa isso? Bom… Vamos supor que eu queira ir de um lugar pra outro, mas o mais importante pra mim não seja a distância entre eles mas o pedágio que vou ter que pagar para pegar cada aresta (estrada). Nesse caso, o peso de cada aresta seria o custo que eu tenho pra passar pela estrada. O problema então seria calcular o caminho onde eu pago menos (o caminho que tem a menor soma de preços) e não o menor caminho no grafo “não-ponderado” (onde consideramos aresta=1 e nada=0).
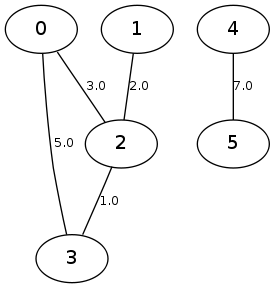
Neste grafo, por exemplo, o menor caminho de 0 a 3 não é a aresta 0–3, mas sim a aresta 0–2 e depois a aresta 2–3.
Para representar um grafo ponderado usando a matriz de adjacência, onde antes marcávamos “1”, marcamos o peso que temos de ir de um vértice para o outro e onde marcávamos “0” marcamos (infinito).
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 3 | 5 | ||||
| 1 | 2 | |||||
| 2 | 3 | 2 | 1 | |||
| 3 | 5 | 1 | ||||
| 4 | 7 | |||||
| 5 | 7 |
Na verdade, só fazemos isso do infinito porque neste caso iríamos querer o menor caminho e o 0 poderia atrapalhar, porque poderíamos ter um caminho sem pedágio, por exemplo, mas isso sempre depende do caso.
Usando listas de adjacência, podemos representar as ligações de cada vértice com dois vetores (um para dizer a qual ele se liga e outro o peso desta ligação) ou com um vetor de structs como:
struct edge {
int destino, peso;
};